In diesem ersten Beitrag zur Theorie möchte ich euch das Thema Spannung, Strom und Leistung näher bringen. Die Art und Weise wie ich dieses Thema erläutere ist vielleicht etwas unkonventionell und wenig akademisch, bietet aber mehr Bezug zur Praxis und räumt mit gängigen „Mythen“ auf.
Allgemeines zur elektrischen Leistung
Leistung ist Arbeit/Energie pro Zeiteinheit. D.h. je mehr Arbeit pro gleicher Zeiteinheit verrichtet wird, umso höher ist die Leistung. Im elektrischen Umfeld wird Arbeit durch eine Kombination von Spannung und Strom verrichtet, z.B. in einfachster Weise durch Umwandlung in Wärme in einem elektrischen Widerstand.
Typisch unterscheidet man bei elektrischen Parametern zwischen Gleichstrom (DC) und Wechselstrom (AC). Dies wird in der Literatur gerne getrennt, da mit jeweils vereinfachten Berechnungsarten gearbeitet wird. Allgemeiner ist folgender Ausdruck:
$p(t) = u(t) \cdot i(t)$
Diese Gleichung beschreibt die Momentanleistung und gilt gleichermaßen für Gleich- als auch Wechselstrom, ist quasi unabhängig von der Kurvenform. Im Falle von Gleichstrom (stationärem Wert für u(t) und i(t)) ergibt sich eine konstante Leistung p(t). Anders bei Wechselstrom, hier schwankt der Wert p(t) periodisch mit Spannung und Strom.
Gleichstrom (DC)
Von Gleichstrom bzw. Gleichspannung (Direct Current) wird dann gesprochen, wenn der arithmetische Mittelwert der Größe einen konstanten, von Null abweichenden Wert hat. Einfacher gesagt: Bei konstanter, gleichbleibender Amplitude.
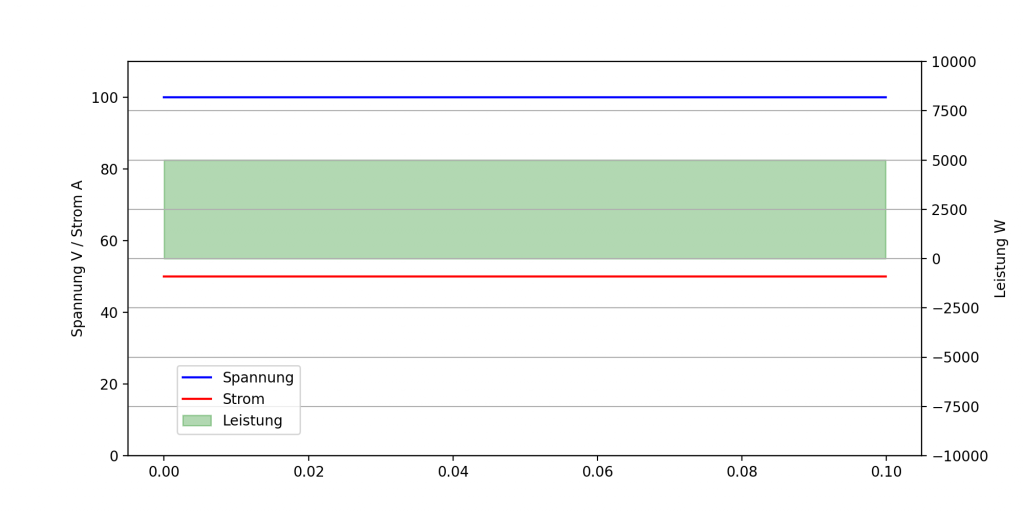
Wechselstrom (AC)
Im Gegensatz dazu, schwingt die Amplitude von Wechselstrom periodisch um den Nullpunkt. Es gibt auch Mischformen von AC & DC. Im Folgenden stelle ich ein Beispiel vor, mit diesen Eckdaten:
- Spannung U = 100 Vrms
- Strom I = 50 Arms
- Frequenz = 50 Hz
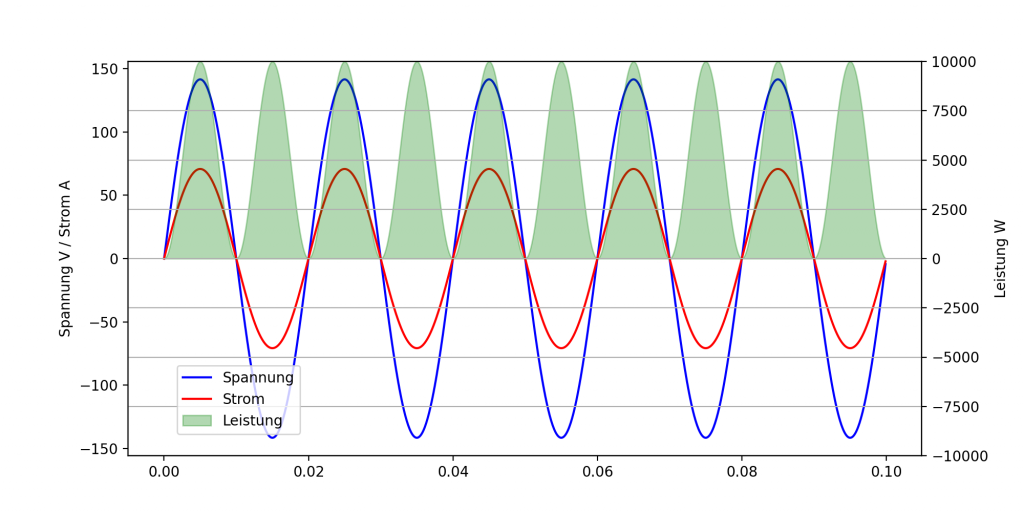
In dieser Grafik erkennt man die periodischen Verläufe von Spannung (in blau), Strom (in rot) und der Leistung (in grün). Die Fläche unter der Leistungskurve ist ein Maß für die übertragene Energie (dazu später mehr). Die Leistung schwankt zwischen 0W und 10000W periodisch mit einer Frequenz von $2 \cdot f$.
Verschiebt sich die „Phase“ zwischen Spannung und Strom (z.B. durch eine kapazitive bzw. induktive Last), ergibt sich ein etwas anderes Bild der Momentanleistung:
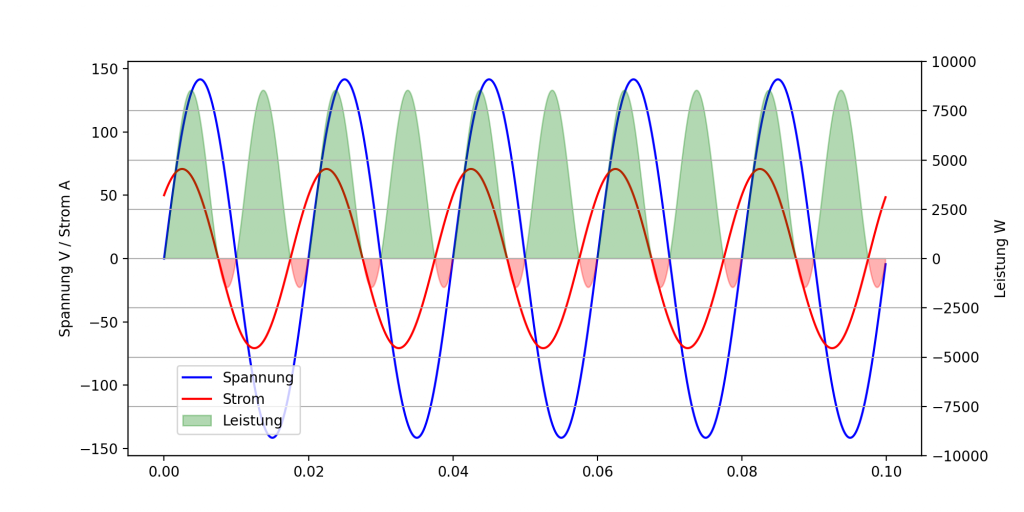
Die Leistung wird zeitweise auch negativ (roter Bereich der Leistungskurve). Das bedeutet, dass sich der Energiefluss teilweise umkehrt. Das schlägt sich in der Blindleistung Q nieder, die nun ungleich Null ist. Diese ist sozusagen der Anteil der Leistung, der zwischen Quelle und Senke periodisch Hin und Her verschoben wird (auch Verschiebungsblindleistung genannt).
Wie viele von uns wissen, zeigen auch Geräte zur Leistungsmessung von AC konstante Werte an. Dazu wird der durchschnittliche Leistungsfluss berechnet, typisch über eine ganzzahlige Periodenanzahl. In unserem Beispiel ergibt sich eine (Wirk-)Leistung von 5000 W (bei Phi = 0°) bzw. 3535 W (bei Phi = 45°). Diese Art der Berechnung kann auf jegliche Kurvenform angewandt werden, d.h. auch Mischformen von AC und DC.
Effektivwert von Spannung und Strom (RMS)
Um Spannung sowie Strom einfache Kenngrößen zuordnen zu können, spricht man bei der Spannungshöhe und Stromstärke meist von Effektivwerten. Dies sind abgeleitete Größen und beschreiben den quadratischen Mittelwert (root mean square, kurz rms), der als Maß für die resultierende Wärmeleistung an einem ohmschen Widerstand gilt, der durch den gleichen Wert einer Gleichspannung oder Gleichstrom hervorgerufen wird. Allgemein kann geschrieben werden:
$Effektivwert = \sqrt{\frac{1}{T}\int_0 ^T{x(t)^2 dt}}$
Wenn $x(t) = sin(2 \cdot \pi \cdot f)$
ergibt das bei T = 1/f folgendes Ergebnis, das man vielleicht schon gut kennt:
$Effektivwert = \frac{1}{\sqrt{2}} = 0.707$
Die Messung von Effektivwerten geschieht meist mit handelsüblichen Multimetern. Einfache Geräte messen den Scheitelwert der Spannung und dividieren diesen durch $\sqrt{2}$, was für viele Fälle ausreichend ist. Bei Mischformen bzw. oberschwingungsbehafteten Signalen, ist das aber nicht mehr zulässig, daher werden mittlerweile meistens Echt-Effektivwert Messgeräte verwendet (true-rms). Diese arbeiten nach der oben genannten Gleichung, sind aber typisch AC-gekoppelt. Das heißt, dieses zeigt bei Gleichstrom bzw. Gleichspannungswerten trotzdem Null an.
Weicht die Kurvenform stark von Gleichspannung oder Sinusförmiger Wechselspannung ab, verliert der Effektivwert seine Aussagekraft. Ein Beispiel seien Frequenzumrichter mit Spannungszwischenkreis, hierbei handelt es sich um „zerhackte“ Gleichspannung. Um dennoch vergleichbare Kennwerte zu erfassen, wird häufig auf die Grundschwingungsbetrachung zurückgegriffen.
Grundschwingungsbetrachtung
Bei der analytischen Berechnung im AC-Bereich wird oft die komplexe Rechnung herangezogen, diese darf aber nur bei rein Sinus-Förmigen Größen angewandt werden (Grundwellenbetrachtung). Warum das so ist, wird in einem weiteren Beitrag zu sehen sein.
Zur visuellen Darstellung verwendet man meist den Einheitskreis mit dem komplexen Zahlensystem, wobei die x-Achse meistens dem Realteil entspricht und die y-Achse dem Imaginärteil. Dabei trägt man dann die Zeiger für Spannung und Strom auf, um eine Relation herzustellen.
Die Phasenverschiebung zwischen zugehörigen U/I Paaren wird meistens mit φ Abgekürzt und entspricht dem eingeschlossenen Winkel zwischen Spannung und Strom: $φ = arg(\underline{U}) – arg(\underline{I})$
Die Leistungen werden dann entsprechend der Effektivwerte sowie der Winkelbeziehung berechnet:
$S = U \cdot I$
$P = U \cdot I \cdot cos(φ)$
$Q = U \cdot I \cdot sin(φ)$
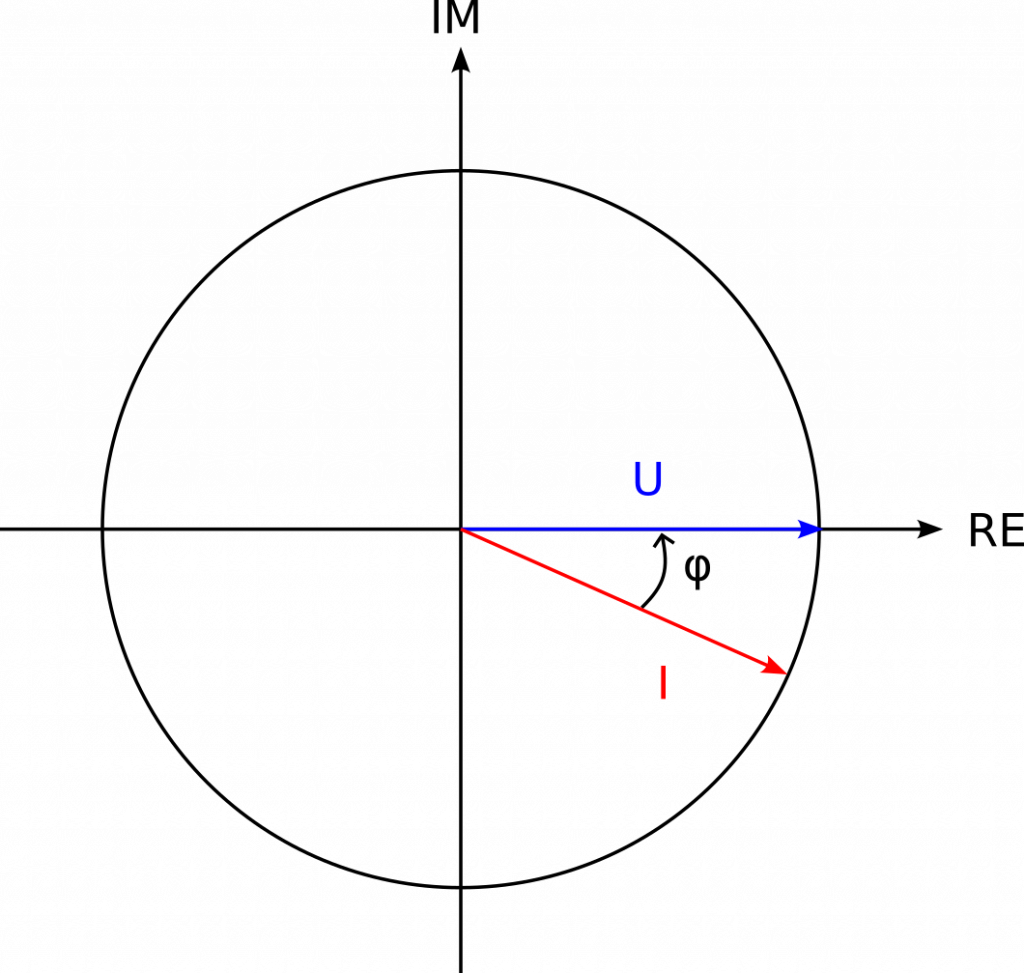
Nicht zu verwechseln ist diese Darstellung mit dem Leistungsdreieck, häufig wird irrtümlich die eine Darstellung in die andere übergeführt, was zu Falschaussagen führen kann. Vor allem das Vorzeichen der Blindleistung wird durch Fehlannahme oft verkehrt angegeben.
Leistungsdreieck
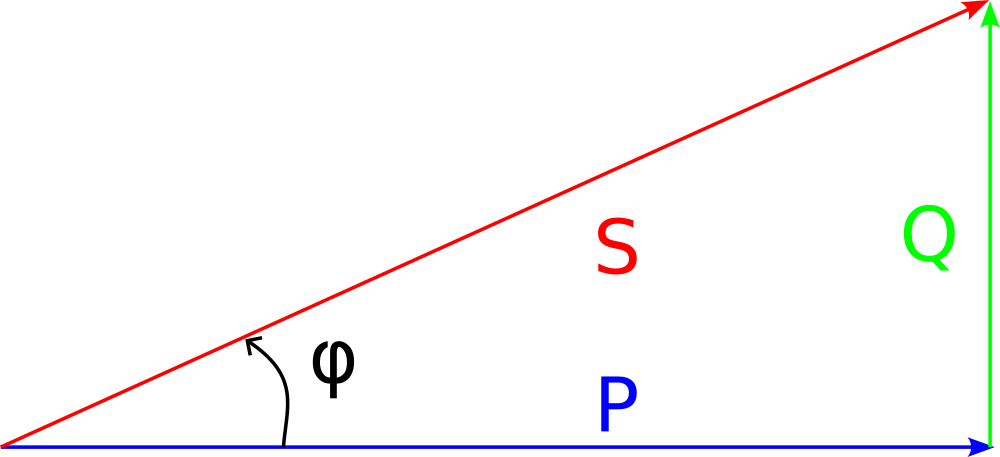
Des weiteren gilt:
$S = \sqrt{P^2 + Q^2}$
$Q = \sqrt{S^2 – P^2}$
Achtung: Q verliert bei dieser Rechenoperation das Vorzeichen und wird deshalb auch als Q_tot für „Total“ bezeichnet.
Leistungsfaktor $PF = cos(φ) = \frac{P}{S}$
Abschließen möchte ich mitgeben, dass das erst ein kleiner Ausflug in die Welt der elektrischen Leistung war, und noch einige Beiträge mit Vertiefungen in verschiedene Richtungen zu erwarten sind. Seien es Mehrphasensysteme, die Rolle von Oberschwingungen oder Energien, lassen Sie sich überraschen oder schreiben Sie mir in einem Kommentar oder per Mail, welches Thema im speziellen für Sie interessant wäre.
Als nächstes wird ein Beitrag über Spannungsqualität erscheinen, um eine solide Grundlage rund um das Themengebiet zu schaffen.
